Es posible que haya oído hablar de la sección áurea en su clase de matemáticas o tal vez se la conozca como la proporción áurea, pero ¿ha oído hablar de la secuencia de Fibonacci? La secuencia de Fibonacci está estrechamente relacionada con la proporción áurea y ocurre con frecuencia en varias facetas de la vida humana. Desde la naturaleza hasta el espacio y el arte, ¡la secuencia de Fibonacci que se discute a continuación es la fórmula para recordar! A continuación se muestra un artículo que lo llevará en un viaje a la secuencia de Fibonacci en el arte, así como responder preguntas como «¿por qué es tan importante la secuencia de Fibonacci?»
¿Qué es la secuencia de Fibonacci?
Cada objeto y persona en el universo se compone de un diseño único, incluyéndote a ti mismo si consideras que no hay dos personas que compartan exactamente la misma composición de ADN. Comúnmente conocida como «código de la naturaleza», la secuencia de Fibonacci se encuentra en el centro de la mayoría de las facetas fundamentales de la existencia humana, incluida la cultura popular.
Documentada por primera vez en el año 300 a.C. por el matemático griego Euclides, la secuencia de Fibonacci es una fórmula matemática que sugiere que cada número es igual a la suma de los dos números que lo preceden.
Numéricamente, la secuencia comienza con los enteros 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, y así sucesivamente, ¡continuando hasta el infinito! La secuencia comienza con un cero, seguido de uno, otro, y por el cuarto dígito, la secuencia comienza sumando el último a los dos para llegar a tres.
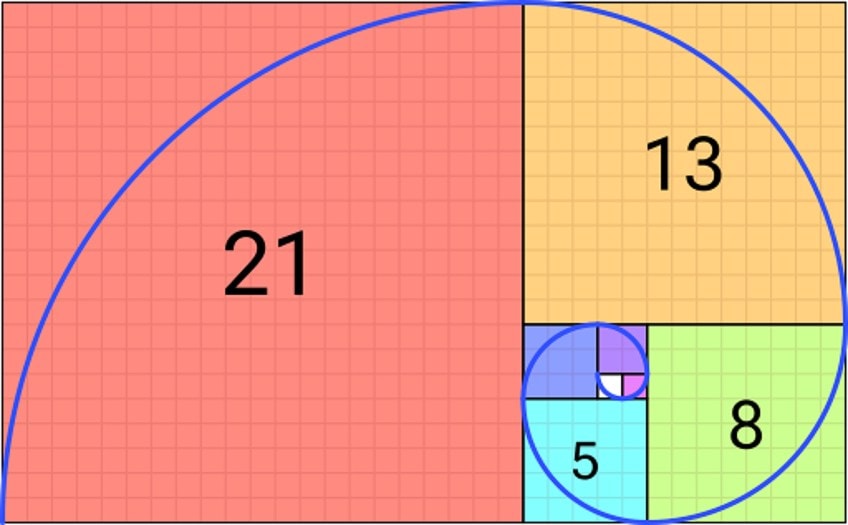Espiral de Fibonacci sobre cuadrados embaldosados; Romain, CC BY-SA 4.0, vía Wikimedia Commons
Aunque esto puede ser confuso para algunos al principio, al echar un vistazo a la representación visual de la secuencia de Fibonacci, reconocerá esto como la proporción áurea (también conocida como la proporción divina). La proporción áurea (1:1.16), como se visualiza en la curva áurea, es un símbolo antiguo que posiblemente ha existido desde el principio de los tiempos.
La proporción áurea se utiliza principalmente en el diseño y se deriva de la secuencia de Fibonacci para producir imágenes estéticas a través de la proporción en el arte, el diseño gráfico y la arquitectura.
Si bien el origen exacto de la secuencia de Fibonacci todavía está en debate, múltiples fuentes afirman que la fórmula fue posiblemente descubierta por el matemático italiano Leonardo Fibonacci mucho después de 1170 dC. Por otro lado, el popular matemático británico, Keith Devlin, afirma que hay hallazgos que datan del año 200 a.C. que consisten en textos dentro de sistemas numéricos hindú-árabes y escritos sánscritos que son anteriores al llamado descubrimiento realizado por Fibonacci.
Un texto publicado por Fibonacci titulado «Liber Abaci», también llamado el «Libro de Cálculo», presentaba métodos para calcular y rastrear las finanzas, para uso de los comerciantes, utilizando la secuencia de Fibonacci.
Un retrato de Leonardo Fibonacci, dibujado antes de 1905; Ver página para autor, dominio público, vía Wikimedia Commons
Leonardo de Pisa usó un ejemplo de conejos donde si se emparejan dos conejos, una hembra y un macho, y se deja que los conejos se reproduzcan, resultará en que una hembra y un macho aparezcan nuevamente en la camada. Usando el macho y la hembra de la primera camada, si esos conejos se reproducen, te quedas con otra camada que contiene otro conjunto de conejos macho-hembra. El ciclo se repite y después de un año, te quedas con alrededor de 144 conejos.
La fórmula aplicada a ese resultado no es, por supuesto, otra que la secuencia de Fibonacci.
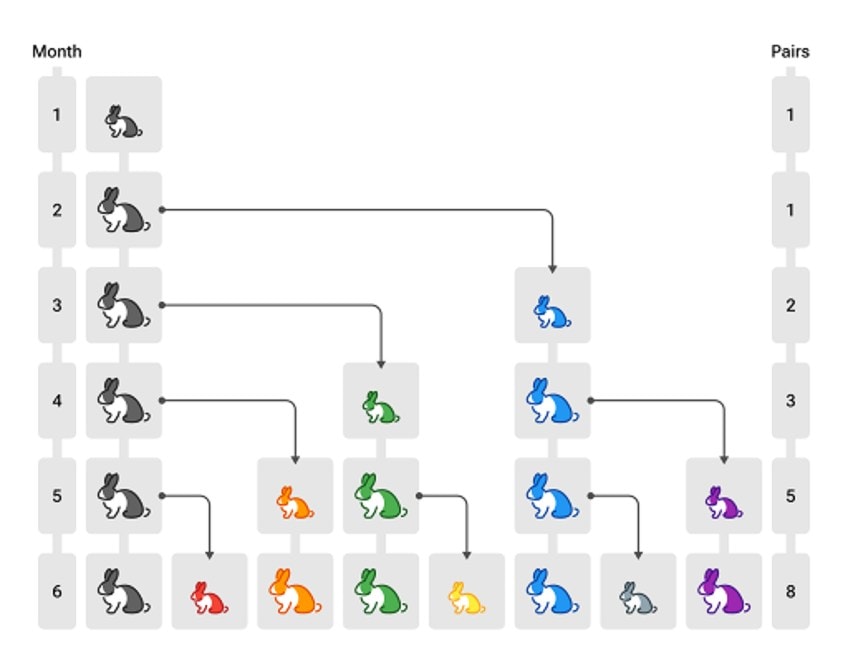Ilustración de la secuencia de Fibonacci en la reproducción de conejos; Romain, CC BY-SA 4.0, vía Wikimedia Commons
¿Para qué se utiliza la secuencia de Fibonacci?
Los números de Fibonacci parecen aparecer en múltiples áreas de la existencia humana, desde sistemas orbitales y plantas hasta ramas de árboles, alcachofas y piñas. La secuencia de Fibonacci también puede estar en el patrón en el que los girasoles generan nuevas células para semillas e incluso en nuestro propio sistema solar, donde la serie de Fibonacci se utiliza para determinar las distancias de las lunas de ciertos planetas como Saturno, Júpiter y Urano. Entonces, ¿por qué es tan importante la secuencia de Fibonacci?
La importancia de la secuencia de Fibonacci radica en la razón por la que es un tema de gran debate.
Entre las razones, la que viene a la palestra es el hecho de que esta fórmula, inicialmente pensada como exclusiva de las matemáticas, se convirtió en una fórmula con una proporción que aparece en elementos muy específicos de la naturaleza; las plantas, el crecimiento de las semillas y el oído humano, y puede considerarse una fórmula universal.
La sección dorada en la naturaleza; Tilnishok, CC BY 4.0, vía Wikimedia Commons
Más evidentemente capturada en los pétalos de las flores, la teoría de Fibonacci en la aplicación de flores muestra que los pétalos de ciertas flores son iguales a los de los diferentes números de Fibonacci. La teoría de Fibonacci también se puede ver un poco más en profundidad con respecto a las flores, coliflores, piñas y plátanos. Aquí nos referimos a la espiral de Fibonacci definida por la organización de las semillas que crecen en las cabezas de las flores en forma de espiral.
El orden de Fibonacci sigue siendo un tema de gran debate, pero sigue siendo muy confiable en su base matemática.
Son solo las especulaciones e hipótesis extraídas del razonamiento detrás de por qué la secuencia aparece en muchos aspectos vitales de la vida humana que se convierte en un tema de debate. Para construir aún más sobre la apariencia del orden de Fibonacci, existe el ángulo dorado. El ángulo dorado sugiere que el ángulo en el que se produce el nuevo crecimiento del crecimiento anterior se encuentra en 222.5 grados y divide un círculo de 360 grados según la sección dorada, que es 0.168 …
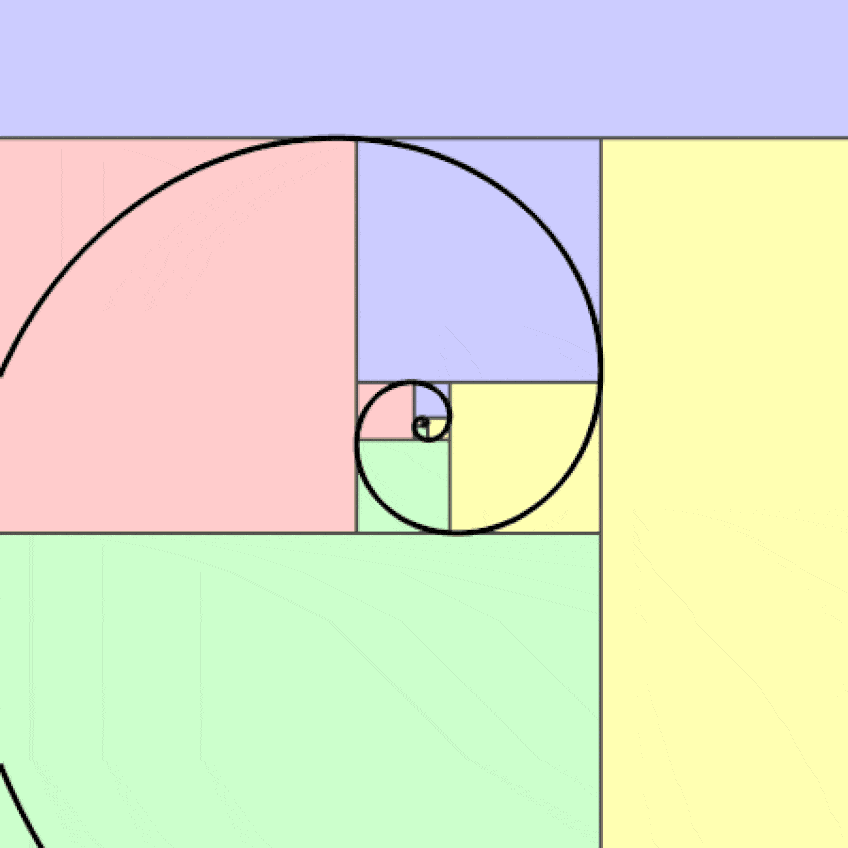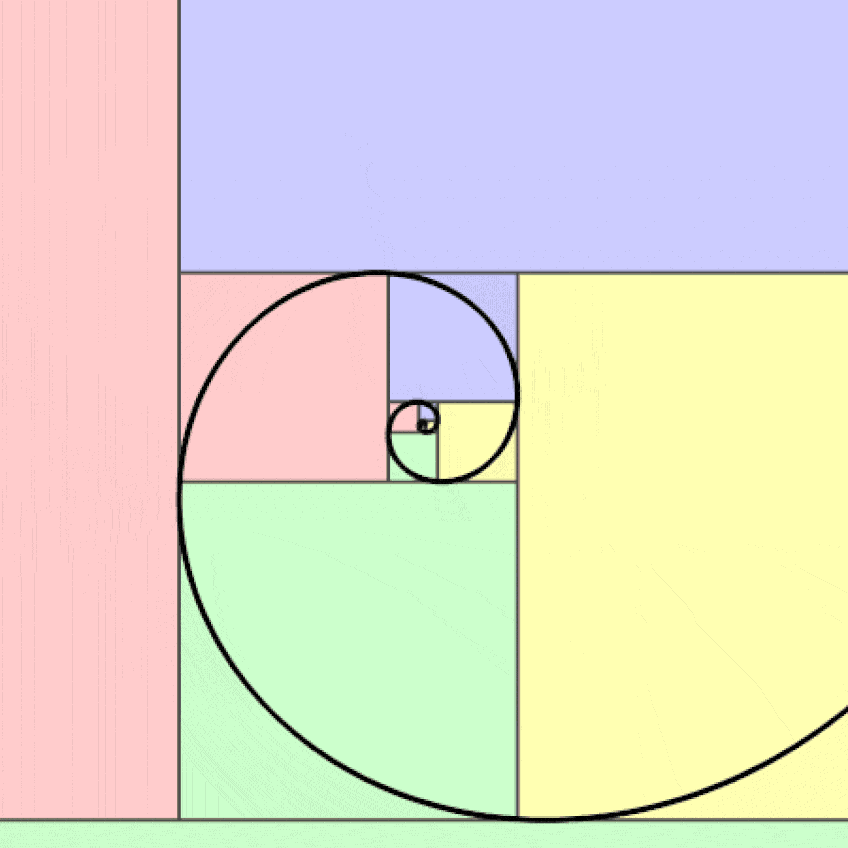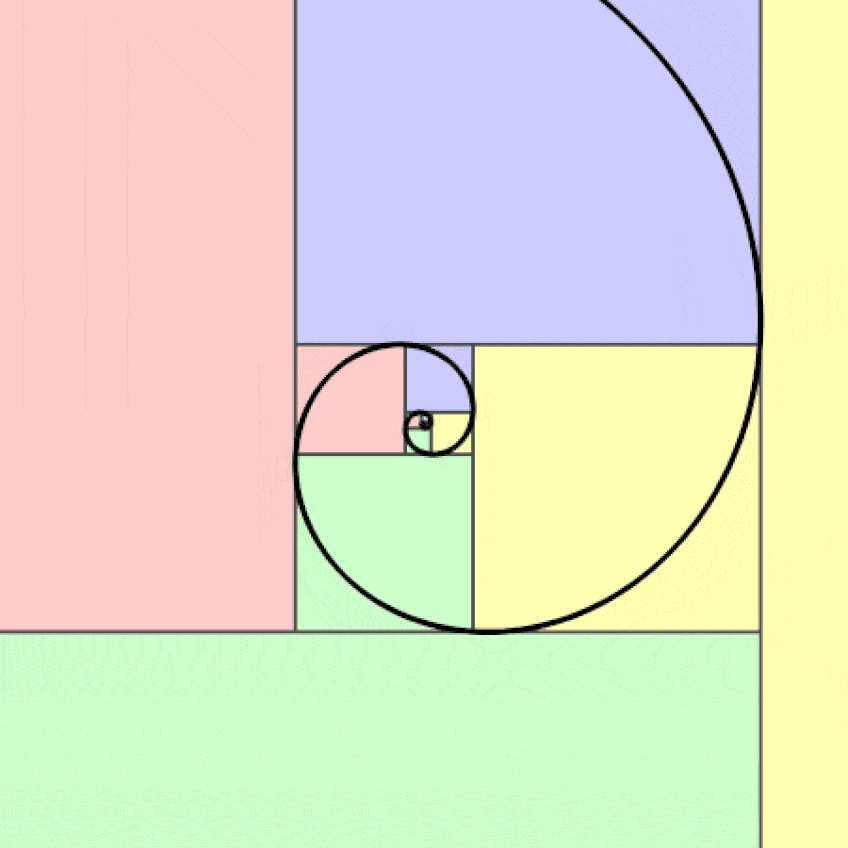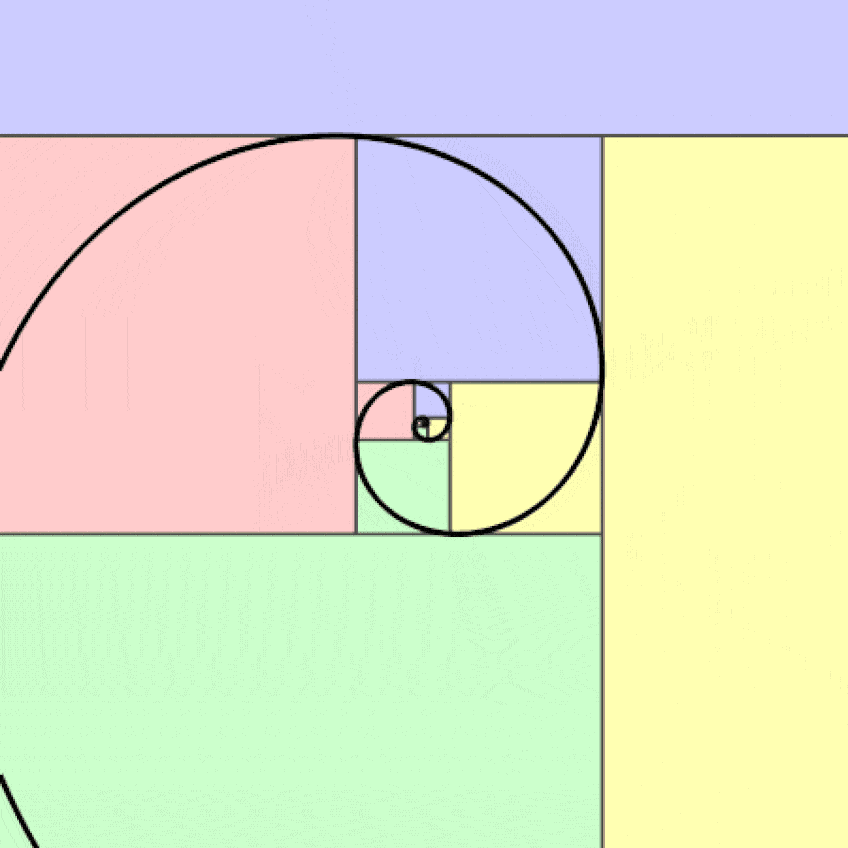Espiral dorada logarítmica; Jahobr, CC0, vía Wikimedia Commons
La regla de los tercios
La regla de los tercios habla directamente de una versión simplificada de la proporción áurea donde es posible un enfoque similar para producir una imagen estéticamente agradable. Desde la fotografía hasta la pintura, la regla de los tercios se aplica dentro del contexto de la composición. Para proceder con la aplicación de la regla de los tercios, primero dividiría su imagen en una cuadrícula de tres por tres y luego colocaría el punto focal de su imagen o pintura, ya sea dos tercios a la izquierda o a la derecha para una imagen horizontal.
La regla de los tercios puede volverse compleja, ¡pero confía en tu ojo para la simetría y no puedes equivocarte! Si se queda atascado, hay programas de software de edición fotográfica como Adobe Lightroom que cuentan con una superposición de proporción áurea como guía para ayudarlo a perfeccionar su composición.
Aplicación de la teoría de Fibonacci
Si bien es útil recurrir a los grandes maestros, también puede ser igual de informativo echar un vistazo más de cerca a algunas de las formas creativas en que los contemporáneos modernos han utilizado la secuencia de Fibonacci a lo largo de la historia del arte.
Aquí hay algunos ejemplos de la secuencia de Fibonacci tal como se practica en la historia del arte para inspirar su aventura en la intersección entre las matemáticas y el arte.
Ejemplos de la secuencia de Fibonacci en el arte
De acuerdo con las ideas neurocientíficas, el ojo humano puede identificar la simetría en 0,05 segundos y sugiere que la simetría, un aspecto de la estética visual dentro de las artes, es algo así como una capacidad inherente a todos. Es el deseo de un atractivo visual armonioso lo que ha informado a muchas de las grandes obras de arte de hoy.
Sección dorada de un mosaico matuliauskas de Cristo en Marijampole, 1997; A Matuliauskas, CC BY-SA 4.0, vía Wikimedia Commons
Doríforo (c. 450 – 440 a. C.) por Policleto
| Artista | Policletos |
| Fecha | c. 450-440 a. C. |
| Dimensiones (cm) | 212 |
| Medio | Mármol |
| Dónde se aloja | Museo Arqueológico Nacional de Nápoles, Nápoles, Italia |
Un ejemplo de arte que llama la atención sobre la simetría se encuentra en una escultura clásica de mármol de un portador de lanza, titulada Doryphoros, esculpida por el escultor griego Polykleitos alrededor de 450-440 aC. Polykleitos, comúnmente conocido como «el Viejo», mostró elegantemente su ojo para la simetría como se muestra en el portador de la lanza.
Se puede decir que la atención de Policleto a la noción de retratar la proporción perfecta del cuerpo humano era una expresión de belleza.
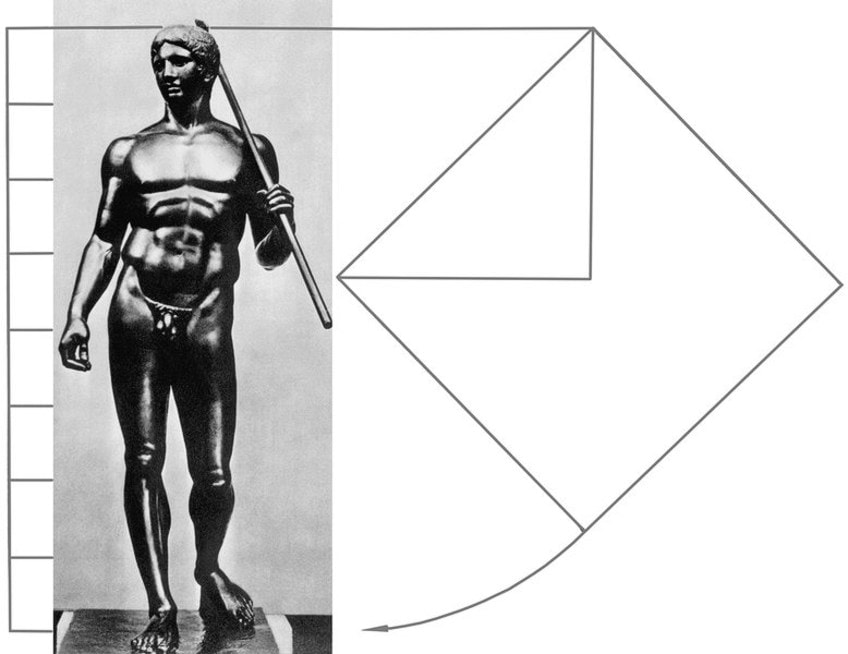Diagrama proporcional que muestra la «figura cuadrada» del Doríforo de Policleto (c. 450-440 a. C.). Reconstrucción por V. G. Vlasov, 1989; Polykleitos, dominio público, vía Wikimedia Commons
Doryphoros de Polykleitos es uno de los ejemplos más sofisticados de arte que incorpora la idea de las matemáticas en la representación de la forma humana, utilizando la perfección en la composición como una medida del «buen arte».
Esta escultura también es anterior a «El hombre de Vitruvio» (c. 1490) de Leonardo da Vinci por casi mil años, absolviendo así la idea deen da Vinci fue el primer y único individuo en impulsar el «pensamiento dorado».
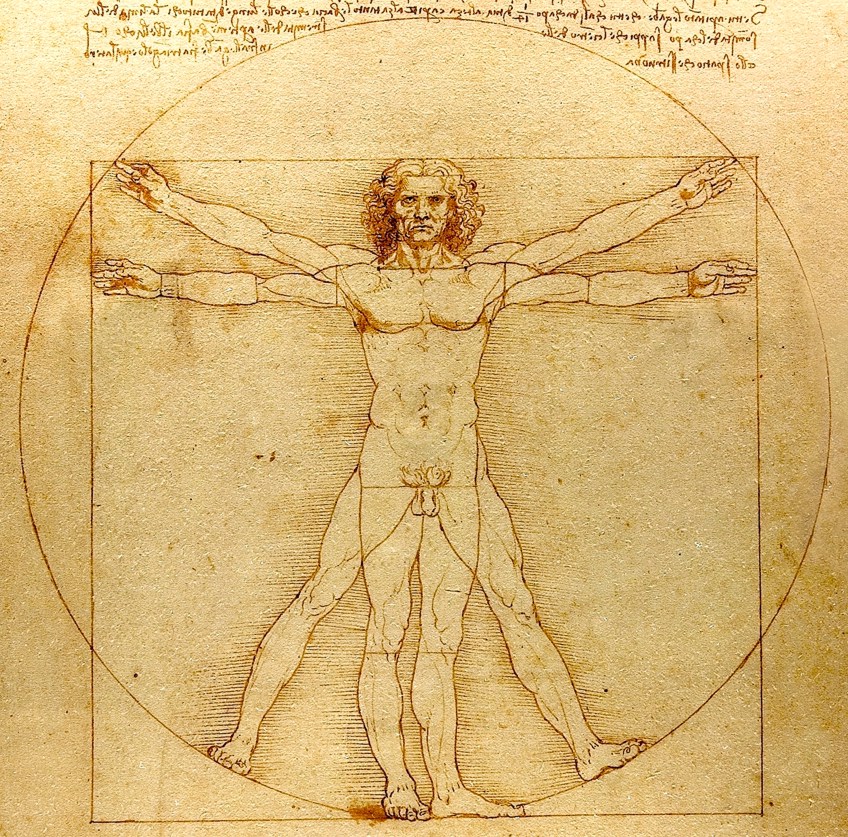El hombre de Vitruvio (c. 1490) de Leonardo da Vinci; Leonardo da Vinci, Dominio público, vía Wikimedia Commons
La Escuela de Atenas (c. 1509 – 1511) por Rafael
| Artista | Raffaello Sanzio da Urbino |
| Fecha | c. 1509-1511 |
| Dimensiones (cm) | 500 x 770 |
| Medio | Óleo |
| Dónde se aloja | Palacio Apostólico, Ciudad del Vaticano, Roma |
Otro artista del Renacimiento italiano que utilizó la secuencia de Fibonacci en el arte es Raffaello Sanzio da Urbino (1483-1520), más conocido como Rafael, cuyas obras fueron una referencia directa al uso de la proporción áurea en la pintura. Junto a artistas de prestigio como Leonardo da Vinci y Miguel Ángel, Rafael produjo un fresco exquisitamente compuesto, La Escuela de Atenas (1509-1511), situado en Stanze di Raffaello del Vaticano.
Estratégicamente colocado en el centro de la pintura se encuentra un rectángulo dorado, lo que indica una referencia potencial al uso del artista de la proporción áurea en la composición.
La Escuela de Atenas (1509-1511) de Rafael, fresco en las Salas de Rafael, Palacio Apostólico, Ciudad del Vaticano; Raphael, Dominio público, vía Wikimedia Commons
Las obras de Rafael hablan por sí solas a través del detalle y la precisión con la que pinta partes clave del fresco. La Escuela de Atenas es definitivamente un excelente ejemplo que destaca el casi hiperenfoque de los grandes maestros en la belleza y el perfeccionismo post-humanismo.
Piet Mondrian y la espiral dorada
Famoso por sus pinturas abstractas, el artista holandés Pieter Cornelis Mondriaan (1872-1944), creó estas coloridas obras de arte, que a primera vista pueden parecer rectángulos y cuadrados aleatorios. A estas alturas, ya deberías haber adivinado: Mondrian hizo bien en incorporar la curva dorada en sus obras que abarcan desde 1918 hasta 1938.
Un ejemplo de esto se puede ver en su pintura de 1921, «Composición con gran plano rojo, amarillo, negro, gris y azul».
Composición con gran plano rojo, amarillo, negro, gris y azul (1921) de Piet Mondrian; Piet Mondrian, dominio público, vía Wikimedia Commons
Ivan Black y la ola cuadrada
El escultor nacido en Londres Ivan Black aplicó la secuencia de Fibonacci a las espectaculares esculturas de onda cuadrada, que cuando están en movimiento, según la ocurrencia natural, la gravedad y el movimiento del titular, cambian para ofrecer varios «movimientos organizados». Estas esculturas móviles, creadas en 2022, se conocen como obras de arte cinéticas, que integran las complejidades de un material altamente calibrado con «formas naturales» como la plaza para ofrecer una experiencia innovadora.
Tal complejidad y precisión, como se espera de una fusión entre el universo matemático y la expresión artística.
Otros ejemplos de la secuencia de Fibonacci
Además del arte, la espiral de Fibonacci también se puede encontrar en muchas otras áreas de estudio. Leonardo da Vinci escribió un famoso libro sobre las proporciones divinas de la proporción áurea en varias disciplinas, y además de esto, ¡la teoría de Fibonacci también se puede aplicar a la música, la arquitectura e incluso al cuerpo humano! Echemos un vistazo.
La rana de Fibonacci (2010) de Alberto Croce; Alberto Croce (Paolo Cuzzoni, Adriano Freri, Massimo Parizzi, Luigi Sansone, Mila Vajani), CC BY-SA 4.0, vía Wikimedia Commons
De Divina Proportione y Leonardo da Vinci
Un colaborador entusiasta de Leonardo da Vinci, Luca Pacioli escribió un libro llamado De Divina Proportione (1509), que detallaba las ideas y hallazgos colaborativos de la aplicación de la proporción áurea en varias disciplinas. El dúo aplicó sus conocimientos matemáticos y creativos a través del alfabeto, la arquitectura, las estructuras e incluso las figuras geométricas.
Da Vinci es uno de los principales pioneros de incorporar la proporción divina en algunas de las pinturas más icónicas del mundo.
El triángulo dorado como se ve en La última cena de Leonardo da Vinci (1498). La leyenda dice «Con [the] triángulo dorado y corte dorado, le recetamos ancho y height de [the] imagen y contornos de la habitación, ancho y alto y lugar para Jesús y [the] apóstoles.»; Marko Cavara, CC BY-SA 4.0, vía Wikimedia Commons
Entre muchas de sus obras se encuentran La Última Cena (1494-1498) y La Jaconde, más conocida como la Mona Lisa (1503-1506). Localizar las proporciones áureas en La Última Cena parece mucho más claro que el de la Mona Lisa. El posicionamiento de la cabeza, el escote, la prenda y el brazo de la Mona Lisa indican algún uso de la proporción áurea.
Aunque no está claro, todavía se puede decir que la anchura de su rostro podría estar muy cerca de la proporción áurea del ancho del lienzo.
La espiral dorada vista en la Mona Lisa o La Jaconde de Leonardo da Vinci (1503); Ellywa, CC BY-SA 4.0, vía Wikimedia Commons
La espiral de Fibonacci y la música
Además de las artes visuales aplicadas, el orden de Fibonacci que ocurre se encuentra en la música. Los números de Fibonacci se pueden encontrar dentro de una de las unidades melódicas centrales, la octava. Si está familiarizado con la octava en un piano, encontrará que la octava consta de 13 notas con cinco teclas negras y ocho blancas. La quinta nota en una escala es también la nota número ocho de 13 notas, formando así la octava. Si tuvieras que dividir ocho por 13… ¡estás en lo cierto! El resultado es aproximadamente 0,61538… ¿Coincidencia u orden?
Incluso uno de los mayores talentos musicales en la historia de la música, Wolfgang Amadeus Mozart, replicó la proporción áurea a través de la disposición de sus sonatas para piano. La octava, como se conoce en términos musicales, es un componente fundamental de la música conocido como un «intervalo único» que informa la base de cómo se escribe e interpreta la música.
¿Qué tan apropiado es que la octava, una unidad musical fundamental, se correlacione con una de las fórmulas más versátiles?
La proporción áurea en relación con la arquitectura
La proporción áurea se puede encontrar dentro de las construcciones de importantes sitios arquitectónicos en todo el mundo. Estos incluyen el Partenón de Grecia y el Edificio de la Secretaría de las Naciones Unidas ubicado en Nueva York. Incluso se dice que la proporción áurea se aplicó a la construcción de las Grandes Pirámides de Giza.
Otros sitios donde se ha encontrado la proporción áurea dentro de la arquitectura incluyen el Taj Mahal, Notre Dame e incluso la Torre Eiffel.
La proporción áurea en general cuando se aplica a la arquitectura es particularmente útil para determinar una proporción apropiada pero equilibrada de ventanas, puertas, diseño y la relatividad de los tamaños a la inclinación del techo para dibujar un edificio u hogar atractivo.
Un paso más allá: rastros de Fibonacci en el cuerpo humano
Has visto ejemplos de la secuencia de Fibonacci aplicada a través de la fotografía, la pintura, la escultura e incluso la música, pero ¿es difícil encontrar los rastros de la teoría de Fibonacci en ti mismo? De nada. La espiral dorada se puede identificar fácilmente en la forma del oído humano, la cóclea, que es biológicamente intrigante si se puede encontrar lo mismo en las cabezas en flor.
Numéricamente, así como la distancia se registra a nivel planetario entre objetos espaciales, también la distancia y los números de Fibonacci se pueden conectar de nuevo a la mano humana.
Con dos manos, cada una con cinco dedos divididos en tres segmentos con dos nudillos cada uno para unir. Todos los cuales son números de Fibonacci. Si eso no es lo suficientemente convincente, la longitud de los huesos encontrados en el brazo humano también equivale a los números de Fibonacci.
Después de deliberar toda esta información que rodea la secuencia de Fibonacci, la proporción áurea y su impacto en las disciplinas fundamentales, ¿se puede decir que la belleza se mantiene literalmente en el ojo del espectador? Dado que las matemáticas son un tema que lleva una seriedad inmensa y un hecho probado, es increíble encontrar la secuencia de Fibonacci aplicada dentro del arte. Deja que esto sea un vistazo a la inmensidad de ideas que pueden surgir de la secuencia de Fibonacci y, con suerte, te inspire a profundizar en las posibilidades que la incorporación de diferentes disciplinas puede aportar a tu práctica artística.
¡Echa un vistazo a nuestra historia web de Fibonacci Spiral aquí!
Preguntas Frecuentes
¿Por qué es tan importante la secuencia de Fibonacci?
Hay muchas razones por las que la aplicación de la secuencia de Fibonacci es tan importante. Las razones principales incluyen su matemática y phImpacto ilosófico en Europa, que informó la fundación de muchas piezas de arte famosas que puede considerar cruciales para el discurso de la historia del arte. Fuera del contexto de la historia del arte, la espiral de Fibonacci también es importante como herramienta y fórmula literal que proporciona un método numérico para expandir la investigación en múltiples campos científicos como la mecánica cuántica, la codificación, la criptografía y la física.
¿Para qué se utiliza la secuencia de Fibonacci?
La secuencia de Fibonacci es una fórmula y referencia matemática utilizada para calcular porcentajes y ratios para su uso por los comerciantes. Alternativamente, se utiliza en diversos campos como el arte, el diseño, la música, el diseño, las finanzas, la arquitectura e incluso las aplicaciones de ingeniería y las estructuras de datos informáticos. Otros usos se encuentran en ingeniería arquitectónica, compresión de audio, comercio e inversiones financieras.
¿Cuál es la diferencia entre la proporción áurea y la secuencia de Fibonacci?
La secuencia de Fibonacci difiere de la proporción áurea en que la proporción para la reducción del intervalo no es constante. La proporción áurea es el resultado de dividir cada figura de la secuencia de Fibonacci por el número anterior. Matemáticamente, F(n) se refiere al enésimo término de la secuencia de Fibonacci y el cociente de F(n)/F(n-1) se establece para acercarse al límite 1.618 con valores crecientes de n. Este límite se denomina proporción áurea.
¿Cuál es la fórmula para calcular el valor de la proporción áurea?
La fórmula para calcular el valor de la proporción áurea es φ (phi) = (1+√5) / 2. En contextos de diseño, la proporción áurea puede ser útil en el diseño de logotipos, formas y diseños estéticos. En cuanto al diseño, la proporción áurea se puede calcular dividiendo su línea en dos partes, lo que garantiza que la línea más larga dividida por la línea más corta equivalga a la suma de ambas partes divididas por la línea larga. Si tiene problemas con los detalles, siempre puede hacer uso de una calculadora de proporción áurea en línea.
¿Qué hace que la espiral de Fibonacci sea diferente de la espiral dorada?
La espiral de Fibonacci se caracteriza por una curvatura discontinua con un ángulo cíclico variable brazo-radio, mientras que la espiral dorada se caracteriza por lo contrario, que es una curvatura continua con un ángulo de radio brazo constante.
¿Quién acuñó el método de la proporción áurea?
La primera persona en describir esta fórmula como la proporción áurea fue Martin Ohm, un matemático alemán que fundó la palabra goldener schnitt en 1835, ahora conocida como la sección áurea.
